How to Read Particle Mean Size?The Meaning?
To describe the particle of the sample powder, one can simply use the median value, D50, or average diameter of particles via mathematical integration. They are the values showed in the test report in the article “How To Read The Report of Particle Size Analysis?” .
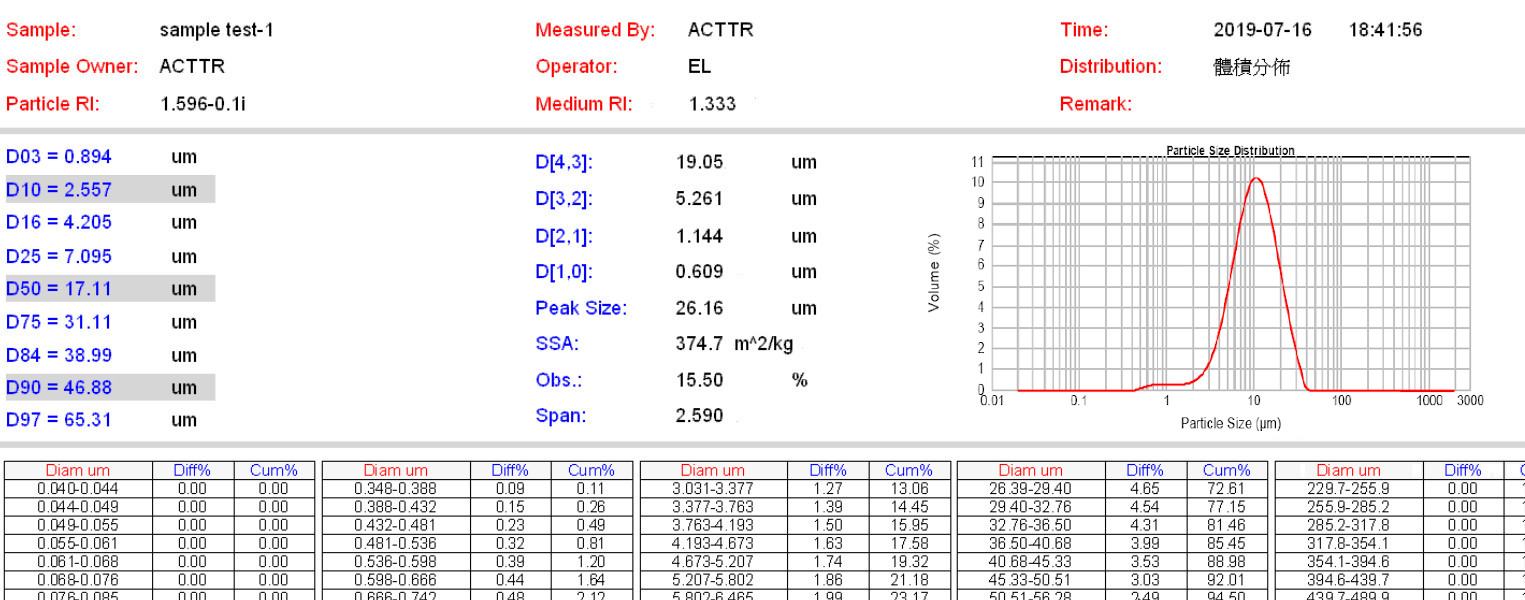
In the particle size analysis report, the four average particle size, D[4,3], D[3,2], D[2,1], D[1,0], is written in the middle the column. “D” represents “Diameter”.
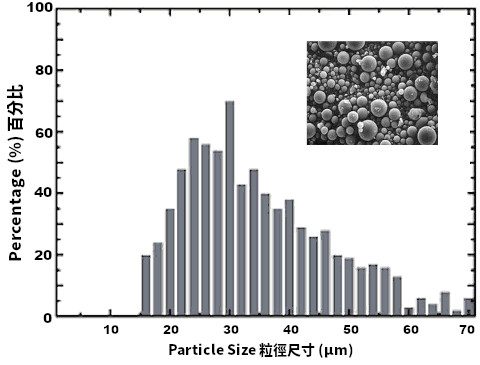
These values come from the particle distribution data, like the graph on the right side of the report, which is a perfect Bezier curve via regression. In the real world, the measurement result from a Particle Size Analyzer is actually like the following histogram (bar chart). The test result of the modern scientific instruments are almost the same analog signal to digital data conversion processes:
These average particle size are calculated by the following formula. You can find the original descriptions in the standard method ASTM E 799:
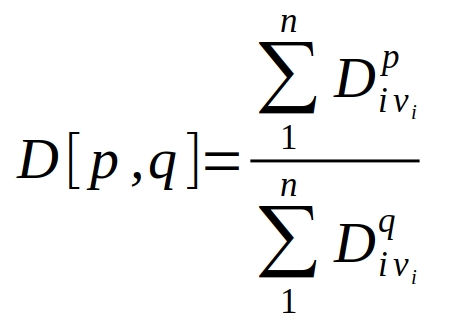
i represents the i-th bar in the histogram. And there are a total of n bars in the graph. And Di is the geometric mean of i-th bar. That is, the square root of upper x lower diameters. For example, the i-th bar means the particles between the diameters of 10um and 11um, it’s geometric mean equals to 10.488 (=sqrt(10*11) in Excel formula).
D[1,0] Average Particle Size
When we sum up the Di * percentage of each bar in the histogram (first power of Di * percentage), we get the total area of integration. After we divide it by the number of bars (sum of zero power of Di), it is actually the concept of arithmetic mean. We can consider D[1,0] as the arithmetic mean particle size. D[1,0] is the basic way to consider the average particle size.
D[4,3] Average Particle Size
D[4,3] is also known as De Brouckere mean, which divides the sum of the fourth power of Di * percentage, divided by third power of the same calculation. D[4,3] averaging, to consider it bluntly, is the concept of volume weighting. D[4,3] is more sensitive to powder samples with more larger particles. The particle size of small particles will be diluted by D[4,3] formula.
D[3,2] Average Particle Size
D[3,2] is also known as Sauter mean. The average of the cubic sum divided by the squared sum will enhance those particles have more consistent value of volume divided by the surface area. That is, those particles with a smoother appearance, will better suit to D[3,2] average.
D[2,1] Average Particle Size
As for D[2,1], it is the best description to those spherical powder, based on the above considerations, because the spherical particles in the laser diffraction 2D projection has better consistent appearance. We can say, the spherical powder in the circular projection at all angles, the diameter are the same. Therefore, D[2,1] average will be closer to the actual particle size of the spherical sample. If your sample looks like spherical under the microscope, D[2,1] will be the best chose to describe the average particle size.
Using one of the above average particle sizes, or using a set of [D10, D50, D90] value can tell others about the particle size characteristics of the sample. However, if you want to describe the particle size of the sample more accurately, you have to choose a suitable average particle size description from the above methods.
ACTTR Technology brought to you the best Particle Size Analyzer from the market. For more detailed product information, please Contact Us!


