平均粒径值要怎么看,有什么意义?
除了 D50 这一个值粒径分布中间值,可以客观说明粒径尺寸之外,也可以用积分算出平均数的表示方法。也就是粒径分析报告中,Peak 上面那四个平均粒径,D[4,3], D[3,2], D[2,1], D[1,0],D 代表 Diameter 直径。
这些粒径平均数值,可以仪器的粒径分析报告中找到。比如,「粒径分析报告与粒径分布曲线要怎么看?」一文中的测试报告结果。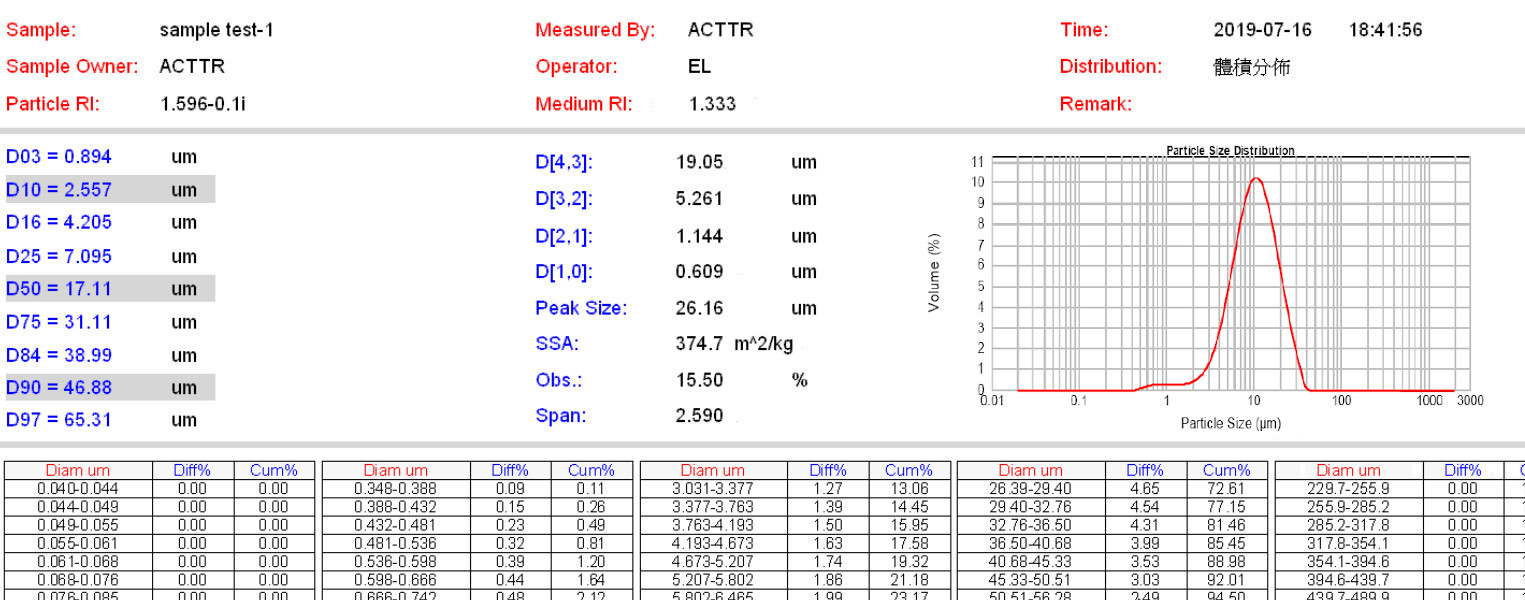
报告中右边的粒度分布图,是经过回归分析计算,所呈现的完美贝兹曲线;仪器实际测量出的结果,其实是像下面这种直方图(histogram,也称为长条图),上方边界线条呈现锯齿状。所有现代仪器设备的测量结果,几乎都是这种类比讯号转换成数位资料的过程:
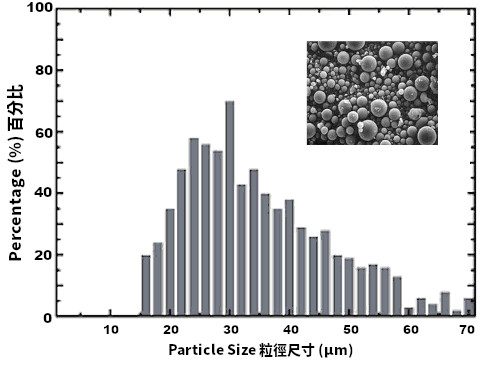
上述这几个平均数值,是由以下公式计算出来的,你可以在标准方法 ASTM E 799 中,找到原文说明:
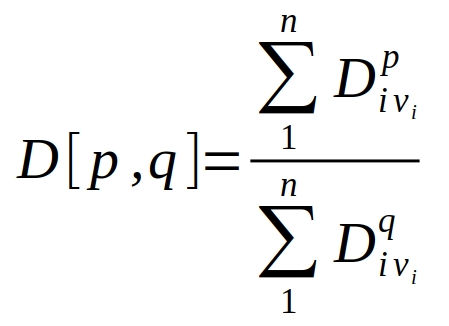
公式中的 i,代表直方图中的第 i 根柱子,图中总共有 n 根柱子,Di代表第i跟柱子粒径的几何平均数,也就是上限粒径x下限粒径的平方根。举例来说,如果第 i 根柱子代表介于10um跟11um之间的颗粒百分数,那么粒径的几何平均数就是(10*11)^0.5,等于10.488。也就是Excel里面 =sqrt(10*11)。
D[1,0] 平均粒径
如果我们把所有柱子的粒径几何平均数x百分比,相当於单一柱子的面积,一个一个数值累加起来,可以得到积分后的总面积,总面积除以柱子的数目,就是我们所了解的算术平均数。 D[1,0] 就是算术平均数粒径,这个平均值,是最基本的平均粒径描述方法。
D[4,3] 平均粒径
D[4,3] 又称为德布鲁克平均直径 (De Brouckere mean),它把每根柱子的几何平均数的四次方,乘以百分比后的总和,除以三次方的和。这种平均方法,说穿了就是体积加权概念。D[4,3] 粒径平均值,对大颗粒偏多的粉末样品比较敏感,小颗粒的粒径尺寸,会被这个多次方乘法的公式淡化掉。
D[3,2] 平均粒径
D[3,2] 又称为索特平均直径 (Sauter mean)。三次方和除以二次方和的平均值,会让体积除以表面积比较一致的粉末,也就是外型比较圆滑一点的粉末,D[3,2] 会更趋近于实际粒径。
D[2,1] 平均粒径
至于 D[2,1],可以想像,适用于球状粉末。因为球状粉末在雷射绕射的 2D投影中,其讯号会更纯净、一致,球状粉末在各个角度的圆形投影,直径长度都一样。因此 D[2,1] 平均粒径值,会更接近球状样品的实际粒径。如果你的样品,在显微镜下,呈现球状,D[2,1]会更适合用来描述你的样品粒径。
用以上某一种平均粒径,或者用一组 [D10, D50, D90] 粒径分布值,都可以告诉他人有关于样品的颗粒尺寸特性。然而,要更准确地描述样品的粒径,让他人一目了然,则需要选用适合的描述方法,以免产生误解。
势动科技为您引进最先进的粒径分析仪器,欢迎联络势动科技,获得最新的产品讯息!


